ABC 414のC問題で回文数に関する問題が出題され、回文数であるかを判定する実装に少し手間取ってしまいました。今後のために、できる限り高速に回文数を判定する方法についてまとめます。

そもそも回文数とは

回文数とは最上位の桁から見ても、最下位の桁から見ても同じになるような数のことです。
つまり自身の桁の並び順を反対にした数と等しいような数といえます。

したがって回文数の判定のためには、まず桁の並びを反対にした数を得るような関数を作りたいです。

桁の並びを反対にした数を得る関数

以下のように、ある数Nを反対にすることはNを10で割り、その余りを最上位の桁から並べていくような操作をNが0になるまで繰り返せばよいです。

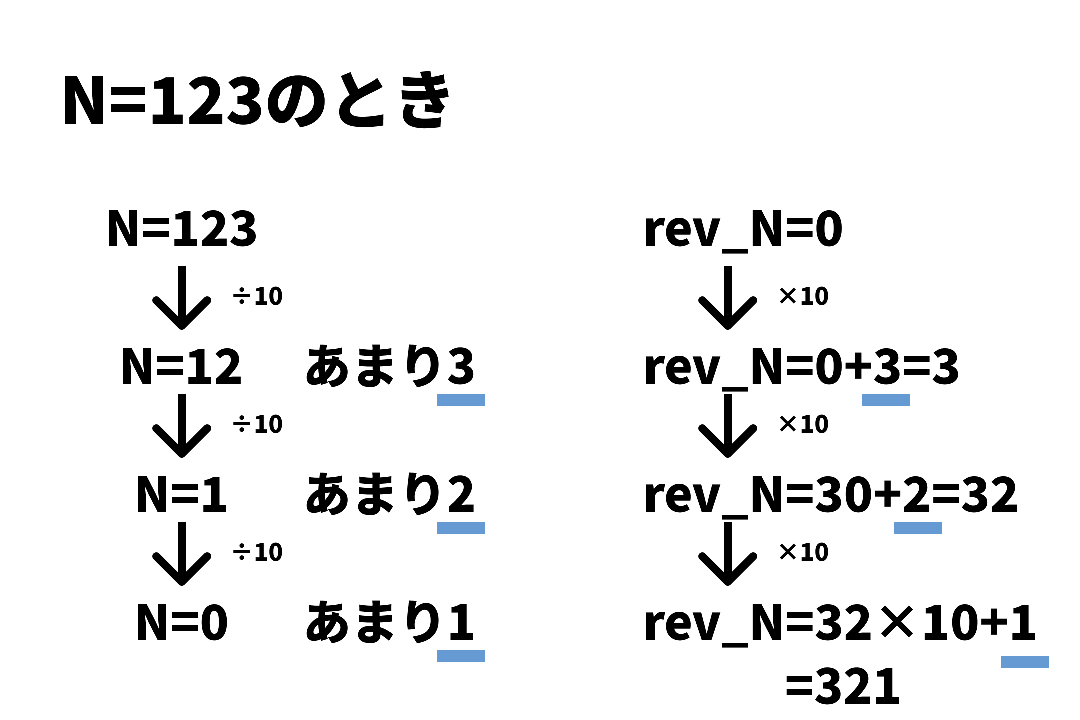
この例では10で割っている、つまり10進数を考えていますがB進数について同様の操作はBで割ることで実現できます。
したがって任意の基数について桁の並びを反対にする関数は以下のようなものになります。

// 基数のデフォルトは10
long long reverse_number(long long n, long long base = 10) {
  long long reversed_n = 0;
  while (n > 0) {
    reversed_n = reversed_n * base + (n % base);
    n /= base;
  }
  return reversed_n;
}

最後に上記の関数を利用することで、任意の基数について回文数であるかの判定は以下のように書けます。

bool is_palindromic(long long n, long long base = 10) {
  return n==reverse_number(n, base);
}

使用例

#include <iostream>
using namespace std;

long long reverse_number(long long n, long long base = 10) {
  long long reversed_n = 0;
  while (n > 0) {
    reversed_n = reversed_n * base + (n % base);
    n /= base;
  }
  return reversed_n;
}

bool is_palindromic(long long n, long long base = 10) {
  return n==reverse_number(n,base);
}

int main() {
  cout<<reverse_number(123)<<endl; // Output : 321
  cout<<is_palindromic(123)<<endl; // Output : 0 (false)

  cout<<reverse_number(121)<<endl; // Output : 121
  cout<<is_palindromic(121)<<endl; // Output : 1 (true)

  cout<<reverse_number(17)<<endl; // Output : 71
  cout<<is_palindromic(17)<<endl; // Output : 0 (false)

  // 17は2進数表記で10001なので、基数を2とすれば回文数
  // 17(10) = 10001(2)
  cout<<reverse_number(17, 2)<<endl; // Output : 17
  cout<<is_palindromic(17, 2)<<endl; // Output : 1 (true)
}